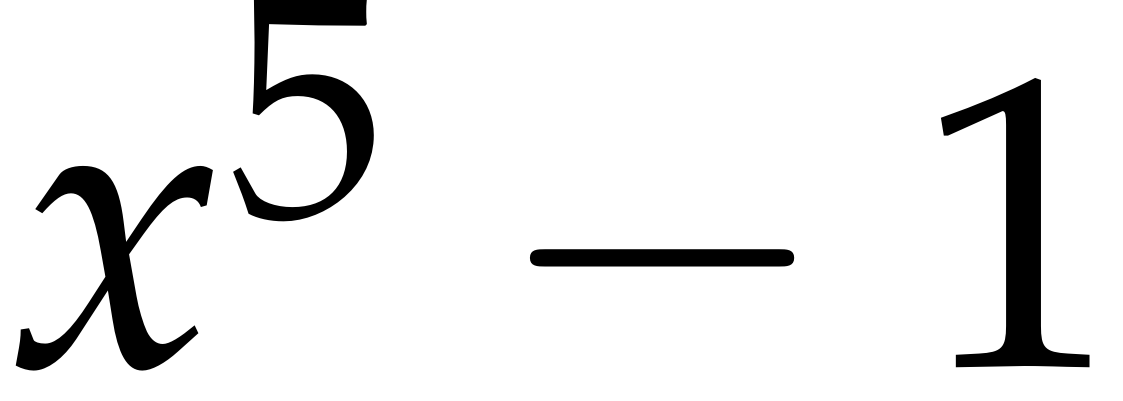
The word game Wordle, invented by Josh Wardle, has seen huge amounts of popularity since its release in October 2021, and numerous variants have appeared, such as Absurdle (adversarial Wordle), Dordle (two linked games of Wordle), Primel (guessing five-digit primes) and Worldle (guessing countries).
I make no attempt to discuss the mathematics of the game as an excellent information theoretic discussion of Wordle has already been produced by 3Blue1Brown here. Instead, I want to jump on the bandwagon and add my own, group theoretic, version of Wordle.
In Wordle, one must guess a five-letter word (of 2315 possible). Notice that there are 26 choices for each of the five spaces (not all of which are valid words). One must do this in six attempts using the information gained at each step (see Wordle's website for the full rules).
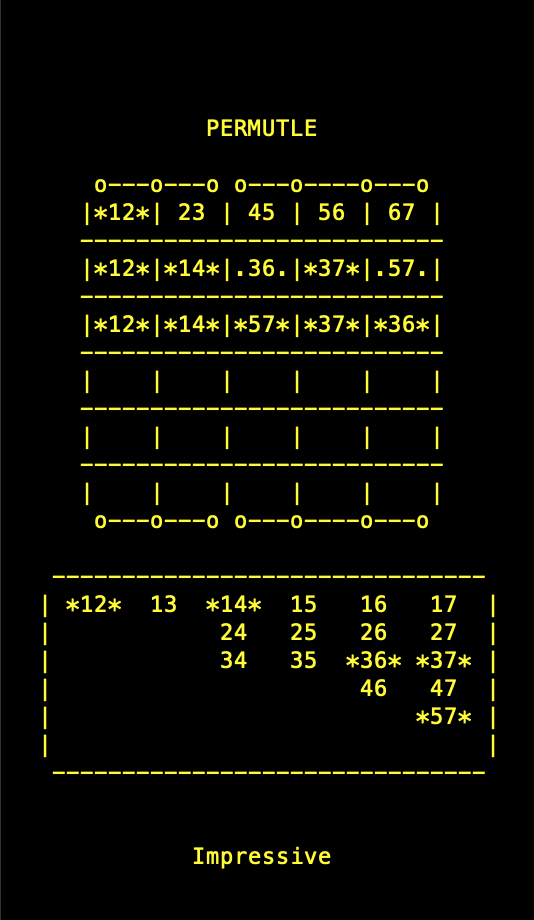
In Permutle, one must put two different numbers between 1 and 7 in each of the five squares such that all seven numbers appear at least once and no numbers are in common between the squares, except there should be exactly one number in common between the 1st and 2nd squares, between the 3rd and 4th squares and the 4th and 5th squares. This is represented by the mnemonic o---o---o o---o----o---o at the top of the game. All other rules are the same as Wordle. I like to think that Permutle is to Wordle as a sudoku is to a crossword.
In fact, Wordle and Permutle are more similar than they appear at first sight. In Permutle, one is is trying to guess a permutation on seven points (rather than a five-letter word, as in Wordle). It's easy to check that a permutation of {1, 2, 3, 4, 5, 6, 7} is uniquely determined by what it does to the five subsets {1, 2}, {2, 3}, {4, 5}, {5, 6}, {6, 7}. Therefore, we can represent such a permutation by sequence of five two-element subsets. Notice that there 5040 possible answers and there are 21 choices for each of the five spaces (not all of which correspond to valid permutations), so the parameters are broadly similar to the original version of Wordle.
For the mathematically curious, ({1, 2}, {2, 3}, {4, 5}, {5, 6}, {6, 7}) is a minimal base for the action of the symmetric group S7 on the set of two-element subsets of {1, 2, 3, 4, 5, 6, 7}, see the survey [Bailey & Cameron, Bull. London Math. Soc. 43, 2011] and the paper [Halasi, Studia Sci. Math. Hungar. 49, 2012] for much more on the subject.
A basic version of this game has been implemented in python.
-
How to play
Save the file permutle.py (from here)
Run python3 permutle.py.
For each turn enter your guess in the form 12 23 45 57 67 then hit enter*.
In particular, for each pair, give the smaller number first.
In the grid:
23 means that 23 is wrong (i.e. grey)
.23. means that 23 is in the wrong place (i.e. yellow)
*23* means that 23 is correct (i.e. green).
Hard mode. To run in hard mode (with the same meaning as in Wordle), run python3 permutle.py -h.
Random games. By default, Permutle gives today's target answer; to receive a random answer, run python3 permutle.py -r (add -h for hard mode).
*In the example given, 12 23 45 57 67 corresponds to guessing that the permutation sends ({1, 2}, {2, 3}, {4, 5}, {5, 6}, {6, 7}) to ({1, 2}, {2, 3}, {4, 5}, {5, 7}, {6,7 }), which in turn corresponds to the permutation that swaps 6 and 7 and fixes the remainder of the points.
Frankly, I think Permutle is much less fun than Wordle. Nevertheless, have fun!