Bernd Schulze
Lancaster University
Thursday 16 November 2023, 4.00pm – 5.00pm
Lecture Theatre D (Mathematical Institute)
Geometric Rigidity, Graphic Statics And Applications
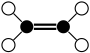
Geometric Rigidity Theory is concerned with the rigidity and flexibility analysis of bar-joint frameworks and related discrete geometric constraint systems. Graphic Statics is a geometric toolbox for structural analysis that is closely linked to Geometric Rigidity. Both of these areas have a rich history which can be traced back to classical work of Euler, Cauchy and Maxwell on the rigidity of polyhedra and skeletal frames.
Over the last two decades or so these subjects have become particularly active, drawing on diverse areas of mathematics, and engaging with a growing range of modern applications, such as Engineering, Robotics, Computer-Aided-Design, Molecular Dynamics, and Materials Science.
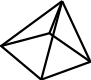
In this talk, I will give an introduction to Geometric Rigidity Theory and Graphic Statics, concentrating on some key combinatorial results and problems for bar-joint frameworks, and on the classical Maxwell-Cremona correspondence between self-stressed frameworks and polyhedral liftings. In the end of the talk, I will show how basic group representation theory can be used to obtain significant additional information about infinitesimal motions, self-stresses and polyhedral liftings of symmetric frameworks. Together with structural engineers from the company SOM, I have recently applied some of these symmetry-based methods to create new design tools for material-efficient long-span structures such as gridhell roofs.
series: Pure Mathematics Colloquium
organiser: Scott Harper