Nick Gill
Open University
Thursday 15 February 2024, 4.00pm – 5.00pm
Lecture Theatre D (Mathematical Institute)
A graph connected to the conjugacy classes of a group and an application to group actions
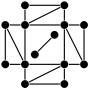
Pierre Guillot, Martin Liebeck and I have recently started studying the following graph: start with a conjugacy class of involutions, C, inside a group G. Define a graph Gr(C) whose vertices are the involutions in C with two vertices, x and y, joined by an edge if the product x.y is also in C.
I will, first, present some results that describe the connected components of the graph Gr(C) for G a member of various families of finite simple group. I will, second, describe how these results relate to celebrated work of Michael Aschbacher and others pertaining to “strongly embedded subgroups”. I will, third, describe how information about the graph Gr(C) can be used to classify the “binary actions” of the group G. (The definition of a “binary action” has its roots in the model theory of Gregory Cherlin – I will define binary actions in the talk!)
series: Pure Mathematics Colloquium
organiser: Scott Harper